비례 배분(Proportional Share) 혹은 공정 배분(Fair Share) 스케줄링은 기존의 스케줄링 알고리즘과는 다른 목적을 가지고 있다. 이전의 알고리즘들이 반환 시간(turnaround time)이나 응답 시간(response time)을 최적화하는 데 중점을 뒀다면, 비례 배분 스케줄링은 각 작업(job)이나 프로세스에게 CPU 시간의 일정 비율을 보장하는 것을 목표로 한다.
비례 배분 스케줄링의 대표적인 예시로는 Waldspurger와 Weihl이 제안한 추첨 스케줄링(Lottery Scheduling)이 있다. 이 아이디어 자체는 상당히 오래되었는데, 그 기본 개념은 매우 간단하다. 다음에 실행할 프로세스를 추첨을 통해 랜덤 하게 선택하되, CPU 시간을 더 많이 할당받아야 할 프로세스에게는 추첨에 당첨될 기회를 더 많이 준다는 것이다.
예를 들어, 두 개의 프로세스 A와 B가 시스템에 존재하고 A는 CPU 시간의 80%를, B는 20%를 받기로 했다고 가정해 본다. 추첨 스케줄링에서는 전체 추첨권(ticket) 100장 중 A에게 80장을, B에게 20장을 부여할 것이다. 그리고 매 스케줄링 시점마다 이 추첨권 중 하나를 무작위로 뽑아, 뽑힌 추첨권을 가진 프로세스를 다음에 실행한다. 이렇게 하면 장기적으로 봤을 때 A와 B가 각각 CPU 시간의 80%, 20%를 할당받을 수 있게 되는 것이다.
기본 개념 : 추첨권이 당신의 지분이다.
추첨권(티켓)이라는 기본적인 개념이 추첨 스케줄링의 근간을 이룬다. 추첨권은 경품권의 개념과 유사하다.
예를 들어, 두 개의 프로세스 A와 B가 시스템에 존재하고 A는 CPU 시간의 75%를, B는 25%를 받기로 했다고 가정해 본다. 추첨 스케줄링에서는 전체 추첨권(ticket) 100장 중 A에게 75장을, B에게 25장을 부여할 것이다. 그리고 매 스케줄링 시점마다 이 추첨권 중 하나를 무작위로 뽑아, 뽑힌 추첨권을 가진 프로세스를 다음에 실행한다. 이렇게 하면 장기적으로 봤을 때 A와 B가 각각 CPU 시간의 75%, 25%를 할당받을 수 있게 되는 것이다.
팁 : 무작위성의 이용
무작위성비례 배분 스케줄링에서 사용되는 추첨권 기반의 무작위 선택 방식은 여러 가지 장점을 가지고 있다. 결정을 내려야 할 때, 이러한 무작위성은 강력하면서도 간단한 해법이 될 수 있다. 전통적인 결정 방식과 비교했을 때, 무작위 방식은 다음과 같은 세 가지 이점을 제공한다.
특수한 상황에 대한 적응력: 무작위 선택은 특이 케이스에 잘 대응한다. 예를 들어, 가상 메모리 시스템에서 많이 사용되는 LRU(Least Recently Used) 페이지 교체 알고리즘은 반복되는 순차 접근 패턴에 대해 최악의 성능을 보이는 경우가 있다. 하지만 무작위로 페이지를 선택하면 이런 최악의 시나리오를 피할 수 있다.
가벼운 구현: 무작위 추첨 방식은 관리해야 할 상태 정보가 매우 적기 때문에 구현이 간단하다. 다른 전통적인 스케줄링 알고리즘들에 비해 알고리즘 자체의 복잡도가 낮은 편이다.
빠른 의사 결정: 난수 생성이 빠르게 이루어진다면, 무작위 추첨을 통한 의사 결정도 신속하게 내려질 수 있다. 이는 스케줄링 결정이 자주 필요한 상황에서 특히 유용하다.
물론 실제 구현에서는 속도 향상을 위해 순수한 무작위성을 어느 정도 포기하고 의사 난수(pseudo-random number)를 사용하기도 한다. 이처럼 무작위성은 비례 배분 스케줄링에 있어 단순한 해법이면서도 강력한 적응력과 효율성을 제공하는 핵심 요소라 할 수 있다. 특히 시스템의 동작을 예측하기 어려운 환경이나, 빠른 의사 결정이 필요한 상황에서 큰 힘을 발휘한다. 물론 무작위 방식이 항상 최선의 선택을 보장하는 것은 아니다. 때로는 특정 프로세스에게 지나치게 불리한 결과를 초래할 수도 있다. 하지만 장기적으로 볼 때, 무작위성은 각 프로세스에게 공정한 기회를 제공하고 특이 상황에 대한 대응력을 높여주는 효과적인 도구임에 틀림없다.
무작위성은 원하는 비율을 정확히 보장하지는 않는다. 하지만 두 작업이 장시간 실행될수록 , 원하는 비율을 달성할 가능성이 높아진다.
추첨 기법
추첨권을 다루는 다양한 기법 중 하나는 추첨권 화폐(ticket currency)의 개념이다. 이 기법은 사용자가 자신의 화폐 가치로 추첨권을 할당하고 이를 자유롭게 변환할 수 있도록 허용한다. 예를 들어, 사용자 A와 B가 각각 100장의 추첨권을 받았다고 가정하면, 사용자 A는 A1과 A2의 두 개의 작업을 실행 중이고 자신이 정한 화폐로 각각 500장의 추첨권을 할당하였다.(전체 1000장의 추첨권 중에). 사용자 B는 하나의 작업을 실행 중이고 자신의 기준 화폐 10장 중에 10장을 할당하였다. 시스템은 A1과 A2의 몫을 A의 기준 화폐 500장에서 전체의 기준이 되는 화폐 각각 50장으로 변환한다. 마찬가지로, B1의 추첨권 10장은 전체 기준이 되는 추첨권 100장으로 변환된다. 전체 기준이 되는 추첨권의 양 (총 200 장을 기준으로 추첨한다.)
다른 유용한 기법은 추첨권 양도(ticket transfer)이다. 이를 통해 프로세스는 추첨권을 일시적으로 다른 프로세스에게 양도할 수 있다. 이는 클라이언트/서버 환경에서 특히 유용하며, 클라이언트 프로세스가 서버에게 작업을 요청할 때 서버의 성능을 최대화하기 위해 추첨권을 전달할 수 있다.
마지막으로, 추첨권 팽창(ticket inflation) 기법은 프로세스가 일시적으로 자신이 소유한 추첨권의 수를 조절할 수 있게 한다. 이는 서로 신뢰하는 프로세스들 간의 상호 작용에서 유용하며, 어떤 프로세스가 더 많은 CPU 시간을 필요로 할 때 다른 프로세스들과 통신하지 않고도 자체적으로 추첨권의 가치를 조절할 수 있다.
구현
추첨 스케줄링의 가장 큰 장점은 구현이 단순하다는 점이다. 필요한 것은 난수 발생기와 프로세스들의 집합을 표현하는 자료 구조(예, 리스트), 추첨권의 전체 개수뿐이다.
// counter: used to track if we’ve found the winner yet
int counter = 0;
// winner: use some call to a random number generator to
// get a value, between 0 and the total # of tickets
int winner = getrandom(0, totaltickets);
// current: use this to walk through the list of jobs
node_t *current = head;
// loop until the sum of ticket values is > the winner
while (current) {
counter = counter + current->tickets;
if (counter > winner)
break; // found the winner
current = current->next;
}
// ’current’ is the winner: schedule it...리스트를 사용하여 프로세스를 관리한다고 가정하자. A, B 및 C 세 개의 프로세스로 구성되고 각자 몇 장의 추첨권을 가진다.

스케줄을 결정하기 위해 먼저 총 추첨권의 개수 $ (400)^{2} $ 중에서 한 숫자를 선택해야 한다. 300이 선택되었다고 하자. 리스트를 순회하며 카운터 값을 이용하여 당첨자를 찾아낸다.
프로세스 리스트를 순회하면서 counter의 값이 winner의 값을 초과할 때까지 각 추첨권 개수를 counter에 더한다. 값이 초과하게 되면 리스트의 현재 원소가 당첨자가 된다. 당첨 번호가 300인 우리의 예에서는 다음과 같이 진행된다. 먼저 A의 추첨권 개수가 더해져서 counter 값이 100으로 증가한다. 100은 300보다 작기 때문에 계속 루프를 실행한다. 다음 counter는 150(B의 추첨권 개수)으로 갱신되고 아직 300보다 작기 때문에 다시 순회를 계속한다. 마침내 counter는 400(확실히 300 보다 큼)으로 갱신되고 루프를 빠져나오게 되고 current는 프로세스 C(당첨자)를 가리키게 된다.
일반적으로 리스트를 내림차순으로 정렬하면 이 과정이 가장 효율적이 된다. 정렬 순서는 알고리즘의 정확성에 영향을 주지는 않는다. 그러나 리스트를 정렬해 놓으면 검색 횟수가 최소화되는 것을 보장한다. 특히, 적은 수의 프로세스가 대부분의 추첨권을 소유하고 있는 경우 효과적이다.
예제
추첨 스케줄링의 동작 원리를 보다 쉽게 이해하기 위해, 두 개의 프로세스가 CPU를 공유하는 상황을 살펴보겠다. 각 프로세스는 동일한 수의 추첨권(예: 100장씩)을 가지고 있고, 수행해야 할 작업량도 같다고 가정한다. 이상적으로는 두 프로세스가 거의 동시에 종료되는 것이 좋겠지만, 추첨 방식의 무작위성 때문에 한 프로세스가 다른 프로세스보다 일찍 끝날 가능성이 있다.
이런 불균형 정도를 측정하기 위해, 간단한 불공정 지표(unfairness metric)인 U를 정의해 보겠다. U는 먼저 종료된 프로세스의 완료 시간을 나중에 종료된 프로세스의 완료 시간으로 나눈 값이다. 예를 들어 첫 번째 프로세스가 시간 10에 끝나고 두 번째 프로세스가 시간 20에 끝났다면, U = 10/20 = 0.5가 된다. 두 프로세스가 거의 동시에 종료될수록 U는 1에 가까워진다. 완벽하게 공정한 스케줄러라면 U = 1을 달성할 것이다.

위 그래프는 프로세스의 실행 시간에 따른 평균 불공정도를 보여준다. 프로세스 실행 시간을 1부터 1000까지 다양하게 변화시키면서 각 경우를 30번씩 시뮬레이션했다. 그래프에서 볼 수 있듯이, 프로세스의 실행 시간이 짧을수록 불공정도가 커지는 경향이 있다. 추첨 스케줄링이 의도한 결과에 근접하려면 프로세스들이 충분히 오랫동안 실행되어야 한다는 것을 알 수 있다.
추첨권 배분 방식
추첨 스케줄링에서 아직 다루지 않은 문제는 추첨권을 작업에게 어떻게 분배할지이다. 작업들에게 몇 개의 추첨권을 주어야 하는지 결정하는 것은 시스템 동작에 큰 영향을 미치므로 상당히 복잡한 문제다. 한 가지 접근 방식은 사용자가 자신의 상황을 가장 잘 이해한다고 가정하는 것이다. 각 사용자에게 추첨권을 할당한 후, 사용자가 자신이 실행하고자 하는 작업에 따라 추첨권을 분배할 수 있도록 하는 것이다. 그러나 이 방법은 문제의 본질을 해결하지 않다. 어떤 작업을 수행해야 하는지 전혀 제시하지 않는다. 주어진 작업 집합에 대한 추첨권 할당 문제는 여전히 해결되지 않은 채로 남아 있다.
왜 결정론적(Deterministic) 방법을 사용하지 않는가
추첨 스케줄링은 무작위성을 활용하여 스케줄러를 단순하면서도 어느 정도 공정하게 만들 수 있지만, 완벽한 비례 배분을 보장하기는 어렵다. 특히 프로세스의 실행 시간이 짧을 때는 이런 한계가 더욱 두드러진다. 이런 문제를 해결하기 위해 Waldspurger는 보폭 스케줄링(stride scheduling)이라는 결정론적 공정 배분 스케줄러를 고안했다.
보폭 스케줄링에서는 각 프로세스마다 고유한 보폭(stride) 값을 할당한다. 보폭은 자신이 가지고 있는 추첨권 수에 반비례하는 값이다. 앞의 예에서 작업 A, B, C는 각각 100, 50, 250의 추첨권을 가지고 있으며 임의의 큰 값을 각자의 추첨권 개수로 나누어 보폭을 계산할 수 있다. 예를 들어 10000을 각자의 추첨권 개수로 나누면 각 작업의 보폭은 100, 200 및 40이 된다. 이 값을 보폭이라고 부르며 프로세스가 CPU를 사용할 때마다 pass 변수를 보폭만큼 증가시켜 CPU 사용량을 추적한다. 스케줄러는 이 pass 값과 보폭을 기준으로 다음에 실행할 프로세스를 결정하게 된다.
기본적인 아이디어는 간단하다. 가장 작은 pass 값을 가진 프로세스를 선택한다. 프로세스를 실행시킬 때마다 pass 값을 보폭만큼씩 증가시킨다. 아래는 Waldspurger가 제시한 보폭 스케줄링의 의사코드다.

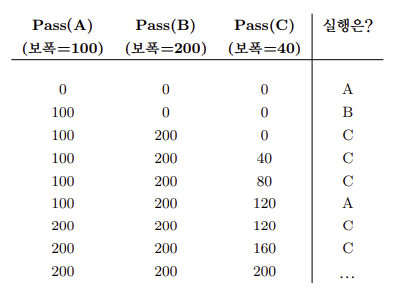
보폭 스케줄링은 이런 방식으로 CPU 사용 시간을 프로세스 간에 공정하게 분배하여, 모든 프로세스가 자신의 중요도에 비례하여 CPU를 사용할 수 있도록 한다.
그런데도 많은 경우 추첨 스케줄링이 선호되는 이유는 무엇일까? 그것은 추첨 스케줄링이 보폭 스케줄링에 비해 가지는 고유한 장점 때문이다.
보폭 스케줄링은 새로운 작업이 도착할 때마다 해당 작업의 상태 정보를 고려하여 스케줄링을 수행한다. 예를 들어 보폭 스케줄링에서 새 작업이 도착하면 해당 작업의 초기 pass 값을 신중히 결정해야 한다. 만약 pass 값을 0으로 설정하면 이 작업이 CPU를 독점할 수도 있다.
반면 추첨 스케줄링에서는 각 작업의 추첨권 수만 관리하면 된다. 새 작업이 추가되면 해당 작업의 추첨권 수를 전체 추첨권 수에 반영하는 것으로 충분하다. 즉, 새 작업을 시스템에 통합하는 과정이 매우 간단해지는 것이다.
또한 추첨 스케줄링은 무작위성으로 인해 특정 패턴의 작업 부하에 대해 보폭 스케줄링보다 더 나은 성능을 보일 수 있다. 물론 정확한 비례 배분이 필요하다면 보폭 스케줄링이 더 적합하겠지만, 많은 실제 시스템에서는 근사적인 공정성으로도 충분한 경우가 많다.
결국 추첨 스케줄링은 구현이 간단하고 새 작업 추가가 용이하며, 무작위성이 주는 이점까지 누릴 수 있어서 여전히 매력적인 선택지로 남아 있는 것이다. 물론 정확성과 공정성 측면에서는 보폭 스케줄링에 뒤질 수밖에 없지만, 그 단순함과 유연함은 실제 시스템을 설계할 때 큰 강점으로 작용할 수 있다.
요약
비례 배분 스케줄링은 시스템 내의 여러 프로세스나 작업들 사이에서 CPU 시간을 공정하게 나누어주는 방식 중 하나다. 이 방식에서는 각 프로세스의 상대적 중요도에 따라 일정 수의 추첨권(ticket)을 부여하는데, 이는 마치 추첨에 응모하는 것과 비슷하다. 추첨권의 수가 많을수록 해당 프로세스가 CPU 시간을 얻을 확률이 높아진다.
스케줄러는 각 프로세스가 가진 추첨권의 수에 비례하여 CPU 시간을 할당한다. 즉, 추첨권을 많이 가진 프로세스일수록 더 자주, 더 오랫동안 CPU를 사용할 수 있게 되는 것이다. 이를 통해 프로세스의 상대적 중요도를 CPU 시간 할당에 공정하게 반영할 수 있다.
비례 배분 스케줄링의 주요 특징은 다음과 같다:
- 상대적 중요도의 반영: 각 프로세스에 할당된 추첨권의 수는 그 프로세스의 중요도를 나타낸다. CPU 시간은 이 추첨권 수에 비례하여 분배되므로, 중요도가 높은 프로세스는 자연스럽게 더 많은 CPU 시간을 받게 된다.
- 유연한 우선순위 조정: 프로세스의 중요도는 추첨권 수를 조정하는 것만으로 쉽게 변경할 수 있다. 새로운 프로세스가 추가되거나 기존 프로세스의 우선순위를 바꿔야 할 때 매우 유용하다.
- 장기적 공정성 보장: 충분히 긴 시간 동안 스케줄링을 수행하면, 각 프로세스는 자신의 추첨권 비율만큼의 CPU 시간을 받게 된다. 이는 시스템 자원이 프로세스 간에 공정하게 분배됨을 의미한다.
하지만 비례 배분 스케줄링에도 몇 가지 단점이 있다. 우선 무작위 추첨 방식 때문에 단기적으로는 CPU 할당이 불균형해 보일 수 있다. 또한 추첨을 수행하고 당첨 프로세스를 확인하는 과정에서 어느 정도의 오버헤드가 발생할 수 있다.
그럼에도 불구하고 비례 배분 스케줄링은 프로세스의 상대적 중요도를 유연하게 반영하면서 시스템 자원을 효율적이고 공정하게 관리할 수 있는 강력한 방법이다. 시스템의 요구사항과 우선순위가 다양한 환경에서 적응력을 발휘할 수 있기에, 여러 분야에서 폭넓게 활용되고 있다.
운영체제의 CPU 스케줄링 알고리즘으로서 뿐만 아니라, 네트워크 대역폭 할당, 디스크 I/O 스케줄링 등 컴퓨터 시스템의 다양한 자원 관리 문제에 비례 배분 스케줄링의 아이디어를 적용할 수 있다. 그만큼 개념이 직관적이고 구현이 간단하면서도 효과적이라고 할 수 있다.
숙제
1. 3개의 작업과 난수 시드 1, 2, 3으로 시뮬레이션한 솔루션을 계산하세요. (계산 과정은 GPT로 정리함)
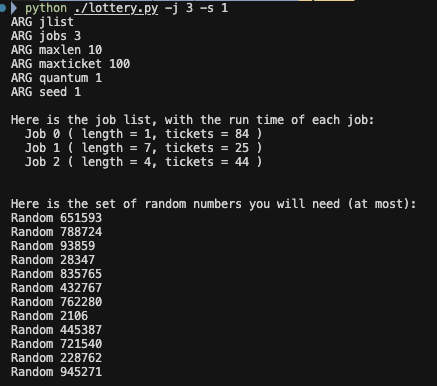
0) 초기 상태
- 작업 목록
- Job 0: length=1, tickets=84
- Job 1: length=7, tickets=25
- Job 2: length=4, tickets=44
- 총 티켓 = 84 + 25 + 44 = 153
- (초기) 티켓 구간
- Job 0: 0 ~ 83 (84장)
- Job 1: 84 ~ 108 (25장)
- Job 2: 109 ~ 152 (44장)
1) 스텝별 계산
[시간 1] R=651593
- 총 티켓=153 → W = 651593 % 153 = 119
- 119는 109~152 구간 → Job 2 선택
- 실행 후 남은 시간: Job2 4 → 3
(아직 아무도 끝나지 않음)
[시간 2] R=788724
- 여전히 총 티켓=153 (아직 아무도 끝나지 않음)
- W = 788724 % 153 = 9
- 9는 0~83 구간 → Job 0 선택
- 실행 후 남은 시간: Job0 1 → 0 → Job 0 완료 (시간 2)
→ 큐에서 제거, 이제 남은 작업은 Job1(25), Job2(44)
(재계산) 현재 총 티켓/구간
- 총 티켓 = 25 + 44 = 69
- 구간
- Job 1: 0 ~ 24 (25장)
- Job 2: 25 ~ 68 (44장)
[시간 3] R=93859
- 총 티켓=69 → W = 93859 % 69 = 19
- 19는 0~24 구간 → Job 1 선택
- Job1 7 → 6
[시간 4] R=28347
- 총 티켓=69 → W = 28347 % 69 = 57
- 57은 25~68 구간 → Job 2 선택
- Job2 3 → 2
[시간 5] R=835765
- 총 티켓=69 → W = 835765 % 69 = 37
- 37은 25~68 구간 → Job 2 선택
- Job2 2 → 1
[시간 6] R=432767
- 총 티켓=69 → W = 432767 % 69 = 68
- 68은 25~68 구간 → Job 2 선택
- Job2 1 → 0 → Job 2 완료 (시간 6)
→ 남은 작업은 Job1(25)뿐
(재계산) 현재 총 티켓/구간
- 총 티켓 = 25
- 구간
- Job 1: 0 ~ 24 (25장) (혼자 남음)
[시간 7] R=762280
- 총 티켓=25 → W = 762280 % 25 = 5
- 유일 후보 → Job 1 선택
- Job1 6 → 5
[시간 8] R=2106
- 총 티켓=25 → W = 2106 % 25 = 6
- Job 1 선택 → Job1 5 → 4
[시간 9] R=445387
- 총 티켓=25 → W = 445387 % 25 = 12
- Job 1 선택 → Job1 4 → 3
[시간 10] R=721540
- 총 티켓=25 → W = 721540 % 25 = 15
- Job 1 선택 → Job1 3 → 2
[시간 11] R=228762
- 총 티켓=25 → W = 228762 % 25 = 12
- Job 1 선택 → Job1 2 → 1
[시간 12] R=945271
- 총 티켓=25 → W = 945271 % 25 = 21
- Job 1 선택 → Job1 1 → 0 → Job 1 완료 (시간 12)
2) 최종 요약 (완료 시각)
- Job 0: 시간 2에 종료
- Job 2: 시간 6에 종료
- Job 1: 시간 12에 종료
- 총 실행 시간 = 1 + 4 + 7 = 12 (퀀텀 12번) — 난수도 정확히 12개 사용됨
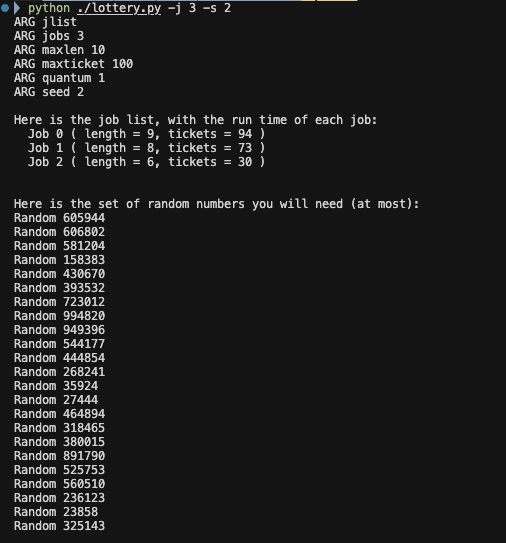
초기 상태
- Job 0: length=9, tickets=94
- Job 1: length=8, tickets=73
- Job 2: length=6, tickets=30
- 초기 Tot = 94+73+30 = 197
- 초기 티켓 구간(0-index, 포함 범위)
- Job 0: 0–93 (94장)
- Job 1: 94–166 (73장)
- Job 2: 167–196 (30장)
스텝별 계산 (t는 1부터 시작; 실행 후 남은 길이 표시)
표기: R(난수), W=R%Tot(당첨 티켓), Run(실행된 잡), left(실행 후 남은 길이)
- t=1: Tot=197, R=605944 → W=169 → Job2 (169∈167–196)
left: j0=9, j1=8, j2=5 - t=2: Tot=197, R=606802 → W=42 → Job0 (42∈0–93)
left: j0=8, j1=8, j2=5 - t=3: Tot=197, R=581204 → W=54 → Job0
left: j0=7, j1=8, j2=5 - t=4: Tot=197, R=158383 → W=192 → Job2
left: j0=7, j1=8, j2=4 - t=5: Tot=197, R=430670 → W=28 → Job0
left: j0=6, j1=8, j2=4 - t=6: Tot=197, R=393532 → W=123 → Job1 (123∈94–166)
left: j0=6, j1=7, j2=4 - t=7: Tot=197, R=723012 → W=22 → Job0
left: j0=5, j1=7, j2=4 - t=8: Tot=197, R=994820 → W=167 → Job2 (167∈167–196)
left: j0=5, j1=7, j2=3 - t=9: Tot=197, R=949396 → W=53 → Job0
left: j0=4, j1=7, j2=3 - t=10: Tot=197, R=544177 → W=63 → Job0
left: j0=3, j1=7, j2=3 - t=11: Tot=197, R=444854 → W=28 → Job0
left: j0=2, j1=7, j2=3 - t=12: Tot=197, R=268241 → W=124 → Job1
left: j0=2, j1=6, j2=3 - t=13: Tot=197, R=35924 → W=70 → Job0
left: j0=1, j1=6, j2=3 - t=14: Tot=197, R=27444 → W=61 → Job0
left: j0=0, j1=6, j2=3 → JOB 0 종료 (t=14)
잡0 종료 후 티켓 재계산
- 남은 작업/티켓: Job1(73), Job2(30) → Tot=103
- 새 구간: Job1 0–72, Job2 73–102
- t=15: Tot=103, R=464894 → W=55 → Job1
left: j0=0, j1=5, j2=3 - t=16: Tot=103, R=318465 → W=92 → Job2 (92∈73–102)
left: j0=0, j1=5, j2=2 - t=17: Tot=103, R=380015 → W=48 → Job1
left: j0=0, j1=4, j2=2 - t=18: Tot=103, R=891790 → W=16 → Job1
left: j0=0, j1=3, j2=2 - t=19: Tot=103, R=525753 → W=41 → Job1
left: j0=0, j1=2, j2=2 - t=20: Tot=103, R=560510 → W=87 → Job2
left: j0=0, j1=2, j2=1 - t=21: Tot=103, R=236123 → W=47 → Job1
left: j0=0, j1=1, j2=1 - t=22: Tot=103, R=23858 → W=65 → Job1
left: j0=0, j1=0, j2=1 → JOB 1 종료 (t=22)
잡1 종료 후 티켓 재계산
- 남은 작업: Job2(30) → Tot=30 (혼자 남음이니 매번 Job2)
- t=23: Tot=30, R=325143 → W=3 → Job2
left: j0=0, j1=0, j2=0 → JOB 2 종료 (t=23)
최종 요약
- 완료 시각: Job0 = t=14, Job1 = t=22, Job2 = t=23
- 총 실행 퀀텀 = 9+8+6 = 23 (난수 23개 모두 사용)
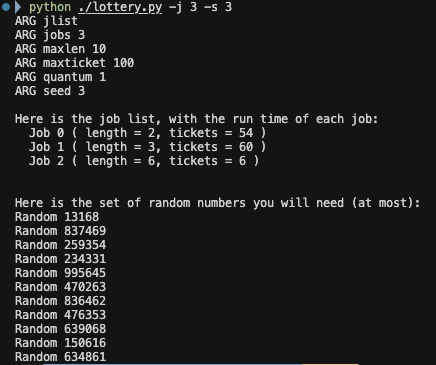
초기 상태
- Job 0: length=2, tickets=54 → 구간 0–53
- Job 1: length=3, tickets=60 → 구간 54–113
- Job 2: length=6, tickets=6 → 구간 114–119
- Tot = 54+60+6 = 120
스텝별 계산
t=1
- R=13168, W=13168 % 120 = 88 → 88 ∈ 54–113 → Job1 실행
- 남은: J0=2, J1=2, J2=6
t=2
- Tot=120, R=837469, W=109 → 109 ∈ 54–113 → Job1 실행
- 남은: J0=2, J1=1, J2=6
t=3
- Tot=120, R=259354, W=34 → 34 ∈ 0–53 → Job0 실행
- 남은: J0=1, J1=1, J2=6
t=4
- Tot=120, R=234331, W=91 → 91 ∈ 54–113 → Job1 실행 → 완료
- 남은: J0=1, J1=0, J2=6
▶ 작업1 완료 후 구간/합 갱신
- 남은 티켓: J0=54(구간 0–53), J2=6(구간 54–59), Tot=60
t=5
- Tot=60, R=995645, W=5 → 5 ∈ 0–53 → Job0 실행 → 완료
- 남은: J0=0, J2=6
▶ 작업0 완료 후 갱신
- 남은 티켓: J2=6(혼자), Tot=6
t=6
- R=470263, W=1 → Job2 (혼자) → 남은 J2=5
t=7
- R=836462, W=2 → Job2 → 남은 J2=4
t=8
- R=476353, W=1 → Job2 → 남은 J2=3
t=9
- R=639068, W=2 → Job2 → 남은 J2=2
t=10
- R=150616, W=4 → Job2 → 남은 J2=1
t=11
- R=634861, W=1 → Job2 실행 → 완료
최종 정리
- 실행 순서(시간 1→11): 1, 1, 0, 1, 0, 2, 2, 2, 2, 2, 2
- 완료 시각
- Job 1: t=4
- Job 0: t=5
- Job 2: t=11
- 총 퀀텀: 2 + 3 + 6 = 11 (난수 11개를 정확히 사용)

2. 이제 두 개의 특정 작업으로 실행해 보세요: 각각 길이는 10이지만 하나(작업 0)는 티켓이 1장이고 다른 하나(작업 1)는 100장입니다(예: -l 10:1,10:100). 티켓의 수가 이렇게 불균형할 때 어떤 일이 일어날까요? 작업 1이 완료되기 전에 작업 0이 실행될 수 있을까요? 얼마나 자주 그럴까요? 일반적으로 이러한 티켓 불균형이 복권 스케줄링의 동작에 어떤 영향을 미칠까요?
A : 작업 1 이 완료되기 전에 작업 0이 실행될 수는 있으나 그 확률이 매우 낮을 것 같다. 대략 10번 중 1 번은 작업 0이 실행될 수 있을 것 같다. 낮은 확률로 실행은 되겠으나 마치 기아현상처럼 보일 것 같다.

3. 길이가 100이고 티켓 할당이 100으로 동일한 두 개의 작업(-l 100:100,100:100)으로 실행할 때 스케줄러는 얼마나 불공정할까요? 몇 가지 다른 난수 시드로 실행하여 (확률적) 답을 결정하세요; 한 작업이 다른 작업보다 얼마나 일찍 끝나는지에 따라 불공정성이 결정됩니다.

난수로 인하여 끝나는 시간이 시드마다 다르다.
'Deep Dive > OS' 카테고리의 다른 글
| [OSTEP] 스터디 6주차 - 메모리 가상화 2 Part.1 (0) | 2025.10.14 |
|---|---|
| [OSTEP] 스터디 5주차 - 메모리 가상화 1 (0) | 2025.09.29 |
| [OSTEP] 스터디 4주차 - 스케줄링 2 : Part.1 - MLFQ (0) | 2025.09.22 |
| [OSTEP] 스터디 3주차 - 스케줄링 1 (0) | 2025.09.15 |
| [OSTEP] 스터디 2주차 - 가상화의 세계 - 숙제 (0) | 2025.09.09 |

