크래프톤 정글

RB-Tree 구현하기 (C언어) - Part.4 삽입 구현

고웅 2025. 4. 22. 08:03

전 포스팅에서 RB-Tree에서의 삽입에 대한 이론적인 설명을 했다. 기본적으로 RB트리도 이진 탐색트리의 일종이기 때문에 삽입에서의 과정은 기존의 이진 탐색트리와 동일하다고 할 수 있다. 이제 다만 삽입 이후 RB-Tree의 조건들을 위반했을 경우 이를 고쳐나가는 fixup 과정이 추가되었다는 것이다.

이 전 글을 보면 RB-Tree에서 fixup을 하는 경우는 크게 3가지로 얘기했다. Case1 ~ 3까지의 경우를 확인하며 이를 수행하는 코드를 작성해 볼 것이다.

2025.04.21 - [크래프톤 정글] - RB-Tree 구현하기 (C언어) - Part.3 삽입 이론 설명

 

RB-Tree 구현하기 (C언어) - Part.3 삽입 이론 설명

RB-Tree의 주요 속성 (5가지 규칙)모든 노드는 레드 또는 블랙이다.루트 노드는 항상 블랙이다.모든 리프 노드(NIL 노드)는 블랙이다.레드 노드의 자식은 반드시 블랙이다.→ 즉, Red 노드는 연속해서

www.gowoong.com

 

1. 구현 목표

RB-Tree의 삽입을 구현하기 위해 크게 4가지 기능을 구현해야 할 것으로 예상 된다.

  1. 삽입 함수 (BST의 삽입을 구현)
  2. fixup 함수 (RB-Tree의 속성을 위반했을 경우 이를 고치기 위함)
  3. 왼쪽 회전
  4. 오른쪽 회전

이제 구현에 들어가 보겠다.

2. 기능 구현

🔨 새로운 값 삽입하기 

node_t *rbtree_insert(rbtree *t, const key_t key) {
    // TODO: implement insert
    return t->root;
}

이 번에도 이전 글들과 같이 구현 코드를 바로 설명하지 않고 어떻게 구현을 해 나가야 할지 구현 아이디어를 먼저 소개하겠다.

구현 아이디어:

  1. 새로 삽입할 노드를 선언하고 동적 메모리 할당을 통해 생성한다.
  2. 생성된 새로운 노드는 RB-Tree의 속성에 맞도록 초기화한다.
    1. 색상은 RED로 시작
    2. 노드가 가지는 부모, 자식들은 nil로 초기화
  3. 현재 노드를 나타내는 cur 선언
  4. 현재 노드가 nil이 될 때까지 반복문을 수행한다.
  5. BST의 삽입과 같이 현재 노드의 키 보다 새로 삽입되는 키 값이 작으면 왼쪽 크면 오른쪽 노드를 현재 노드로 설정한다.
  6. 모든 반복이 끝이 나면 (삽입할 위치 결정)
  7. 새로운 노드의 부모 노드를 현재 노드로 설정한다.
  8. 만약 현재 노드가 nil이었다면(최초 삽입의 경우) 그냥 노드를 삽입한다.
  9. BST 삽입은 완료했으나 RB-Tree의 속성을 만족하는지 확인하고 수정하기 위해 fixup 함수를 호출한다.
  10. 수정이 완료된 트리의 root를 반환
더보기 
node_t *rbtree_insert(rbtree *t, const key_t key) {
    // TODO: implement insert
    node_t *new_node = (node_t *)calloc(1, sizeof(node_t));
    if (new_node == NULL) {
        return NULL;
    }
    new_node->key = key;
    new_node->color =RBTREE_RED;
    new_node->left = t->nil;
    new_node->right = t->nil;
    new_node->parent = t->nil;

    node_t *cur = t->root;
    while (t->nil != cur) {
        if (key < cur->key) {
            if (cur->left == t->nil) {
                cur->left = new_node;
                break;
            }
            cur = cur->left;
        }else {
            if (cur->right == t->nil) {
                cur->right = new_node;
                break;
            }
            cur = cur->right;
        }
    }

    new_node->parent = cur;

    if (cur == t->nil) {
        t->root = new_node;
    }
    // RB tree 케이스 처리 함수......
    rb_insert_fixup(t, new_node);
    return t->root;
}

더 보기를 통해 구현한 코드를 확인할 수 있다.

🔨 삽입 후 수정하기

void rb_insert_fixup(rbtree *t, node_t *target) {
}

fixup함수는 새로 삽입했던 노드를 기준으로 RB-Tree의 속성 위반을 고쳐나가는 함수이다.

구현 아이디어:

  1. 반복문 while 사용 - 삽입하는 노드의 부모 노드의 색깔이 RED인 경우 반복 계속
  2. 편리하게 작성하기 위해 parent, grandparent라는 변수 선언
  3. 조건문 if (부모 노드가 할아버지 노드의 왼쪽 자식인 경우)
    1. 삼촌 uncle 노드를 선언하고 해당되는 값을 설정
    2. 조건문 if ( 삼촌의 색깔이 RED 인 경우) -> case 1 
      1. 부모의 색상을 black으로 바꾸고 삼촌의 색상도 black으로 바꾼다. 반면 할아버지의 색상을 RED로 바꾼다.
      2. 할아버지 노드를 새로운 타깃으로 설정한다.
    3. 조건문 else (삼촌의 색깔이 Black인 경우)
      1. 조건문 if (본인- target 이 부모의 오른쪽 자녀인 경우) -> case 3
        1. 부모를 대상으로 설정한다.
        2. 부모를 기준으로 왼쪽으로 회전한다.
        3. 할아버지를 새로운 부모로 설정한다. -> 회전으로 현재 부모의 위치가 변경되었기 때문
      2. 부모의 색깔을 Black으로 설정한다.
      3. 할아버지의 색깔을 RED로 바꾼다.
      4. 할아버지 노드를 기준으로 오른쪽으로 회전한다. -> case 2
  4. 조건문 else (부모 노드가 할아버지 노드의 오른쪽 자식인 경우) 
    1. 위의 조건을 반대로 하여 작성한다.
  5. while 반복이 종료되면 즉 더 이상 수정할 노드가 없거나 노드가 루트 노드에 도달한 경우 root 노드의 색깔을 Black으로 설정한다.

더 보기를 통해 구현된 코드를 확인할 수 있다.

더보기 
void rb_insert_fixup(rbtree *t, node_t *target) {
    while (target->parent->color == RBTREE_RED) {
        node_t *parent = target->parent;
        node_t *grandparent = parent->parent;
        if (grandparent->left == parent) {
            // 부모 노드가 할아버지 노드의 왼쪽 자식일 경우
            node_t *uncle = grandparent->right; // 삼촌 노드
            if (uncle->color == RBTREE_RED) { //case 1
                parent->color = RBTREE_BLACK;
                uncle->color = RBTREE_BLACK;
                grandparent->color = RBTREE_RED;
                target = grandparent;
            } else{
                if (target == parent->right) {
                    // 부모가 오른쪽 자식이면 left-rotation
                    target = parent;
                    rb_left_rotation(t, target);
                    parent = target->parent;
                }
                parent->color = RBTREE_BLACK;
                grandparent->color = RBTREE_RED;
                //right_rotation
                rb_right_rotation(t, grandparent);
            }
        }
        else {
            // 부모 노드가 할아버지 노드의 오른쪽 자식일 경우
            node_t *uncle = grandparent->left; // 삼촌 노드
            if (uncle->color == RBTREE_RED) { //case 1
                parent->color = RBTREE_BLACK;
                uncle->color = RBTREE_BLACK;
                grandparent->color = RBTREE_RED;
                target = grandparent;
            } else{
                if (target == parent->left) {
                    // 부모가 왼쪽 자식이면 right-rotation
                    target = parent;
                    //right_rotation
                    rb_right_rotation(t, target);
                    parent = target->parent;
                }
                parent->color = RBTREE_BLACK;
                grandparent->color = RBTREE_RED;
                //left_rotation
                rb_left_rotation(t, grandparent);
            }
        }
    }
    t->root->color = RBTREE_BLACK;
}

🔨 왼쪽 회전 

왼쪽 회전을 구현하겠다.

void rb_left_rotation(rbtree *t, node_t *pivot) {
}

구현 아이디어 :

  1. 왼쪽 회전의 경우 부모 노드와 그 오른쪽 자녀에 대해서 수정이 일어나기 때문에 right_child라는 변수를 선언하고 pivot 노드의 오른쪽 자식을 설정
  2. 회전을 수행할 때 right_child의 왼쪽 자식들 즉 베타에 있는 자식들을 피봇 대상 노드 X의 오른쪽 자식으로 연결한다.
  3. 조건문 if (right_child)의 왼쪽 자식이 nil이 아닌 경우
    1. nil노드가 아닌 경우 pivot의 오른쪽에 연결하기 위해 현재 선택한 노드의 부모를 pivot으로 바꾼다.
  4. 기존 노드 X의 부모를 Y 노드의 부모로 설정한다.
  5. 이때 X의 부모가 nil이었을 경우 즉 X가 루트 노드였을 경우 Y노드를 새로운 루트 노드로 설정한다.
  6.  조건문 else if (피봇 되는 노드가 피봇 노드 부모의 왼쪽 자식인 경우)
    1. 피봇 되는 노드의 부모 노드의 왼쪽 자식을 right_child로 재 조정
  7. 조건문 else (피봇되는 노드가 피봇 노드 부모의 오른쪽 자식인 경우)
    1. 파봇 되는 노드의 부모 노드의 오른쪽 자식을 right_child로 재 조정
  8. right_child의 왼쪽 자식을 pivot으로 설정
  9. 피봇 노드의 부모를 right_child로 설정한다.
더보기 
void rb_left_rotation(rbtree *t, node_t *pivot) {
    node_t *right_child = pivot->right;
    pivot->right = right_child->left;
    if (right_child->left != t->nil) {
        right_child->left->parent = pivot;
    }
    right_child->parent = pivot->parent;
    if (pivot->parent == t->nil) {
        t->root = right_child;
    }
    else if (pivot == pivot->parent->left) {
        pivot->parent->left = right_child;
    }
    else {
        pivot->parent->right = right_child;
    }
    right_child->left = pivot;
    pivot->parent = right_child;
}

완성 코드는 더 보기를 통해 확인할 수 있다.

🔨 오른쪽 회전 

왼쪽 회전을 구현하겠다.

void rb_right_rotation(rbtree *t, node_t *pivot) {
}

구현 아이디어 :

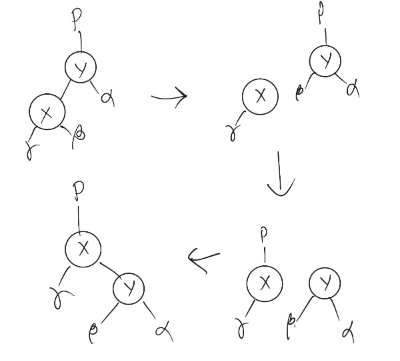
  1. 오른쪽 회전의 경우 부모 노드와 그 왼쪽 자녀에 대해서 수정이 일어나기 때문에 left_child라는 변수를 선언하고 pivot 노드의 왼쪽 자식을 설정
  2. 회전을 수행할 때 left_child의 오른쪽 자식들 즉 베타에 있는 자식들을 피봇 대상 노드 X의 왼쪽 자식으로 연결한다.
  3. 조건문 if (left_child)의 오른쪽 자식이 nil이 아닌 경우
    1. nil노드가 아닌 경우 pivot의 왼쪽에 연결하기 위해 현재 선택한 노드의 부모를 pivot으로 바꾼다.
  4. 기존 노드 X의 부모를 Y 노드의 부모로 설정한다.
  5. 이때 X의 부모가 nil이었을 경우 즉 X가 루트 노드였을 경우 Y노드를 새로운 루트 노드로 설정한다.
  6.  조건문 else if (피봇 되는 노드가 피봇 노드 부모의 왼쪽 자식인 경우)
    1. 피봇 되는 노드의 부모 노드의 왼쪽 자식을 left_child로 재 조정
  7. 조건문 else (피봇되는 노드가 피봇 노드 부모의 오른쪽 자식인 경우)
    1. 파봇 되는 노드의 부모 노드의 오른쪽 자식을 left_child로 재 조정
  8. left_child의 오른쪽 자식을 pivot으로 설정
  9. 피봇 노드의 부모를 left_child로 설정한다.
더보기 
void rb_right_rotation(rbtree *t, node_t *pivot) {
    node_t *left_child = pivot->left;
    pivot->left = left_child->right;
    if (left_child->right != t->nil){
        left_child->right->parent = pivot;
    }
    left_child->parent = pivot->parent;
    if (pivot->parent == t->nil){
        t->root = left_child;
    }
    else if (pivot == pivot->parent->right){
        pivot->parent->right = left_child;
    }
    else{
        pivot->parent->left = left_child;
    }
    left_child->right = pivot;
    pivot->parent = left_child;
}

완성 코드는 더 보기를 통해 확인할 수 있다.

 

저작자표시 동일조건