AVL 트리 개념 정리

이 전 포스팅으로 이진 탐색 트리나, RED-BLACK TREE를 살펴봤다. 이진 탐색 트리의 비효율성을 개선하기 위해 균형 이진 탐색 트리(Balanced Binary Search Tree)의 개념이 등장했고 RB-Tree가 이 균형 이진 탐색 트리의 종류 중 하나였다. 이번에는 또 다른 균형 이진 탐색 트리인 AVL 트리에 대해 정리하겠다.

---

AVL 트리란?

AVL 트리라는 이름은 이 자료구조를 만든 두 사람, Adelson-Velsky와 Landis의 이름을 따서 지어졌다.

• 모든 노드에 대해 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이가 1 이하인 이진 탐색 트리(BST)이다.
• 이 높이 차이를 균형 인수(Balance Factor)라고 하며,

Balance Factor=(left subtree height)−(right subtree height)

• 값은 반드시 -1, 0, 1 중 하나여야 한다.

AVL 트리 예시

---

왜 필요한가?

• 일반적인 BST는 삽입 순서에 따라 편향되면 성능이 O(n)까지 떨어질 수 있음
• AVL 트리는 삽입/삭제 시 항상 균형 유지를 통해 성능을 O(log n)으로 보장함

주요 특징

특징	내용
균형 조건	각 노드의 좌우 서브트리 높이 차이가 -1, 0, 1
삽입/삭제 후	균형 조건을 위반하면 회전을 통해 트리 재구성
탐색 시간	O(log n)
삽입/삭제 시간	O(log n)

AVL 트리 연산 시 필요한 회전(Rotation)

트리 균형을 맞추기 위한 회전이 4가지 존재함:

1. LL 회전 (단순 우회전)
   • 왼쪽 자식의 왼쪽 서브트리에 삽입된 경우

계속 우려먹는 오른쪽 회전 예시

1. RR 회전 (단순 좌회전)
   • 오른쪽 자식의 오른쪽 서브트리에 삽입된 경우

계속 우려먹는 왼쪽 회전 예시

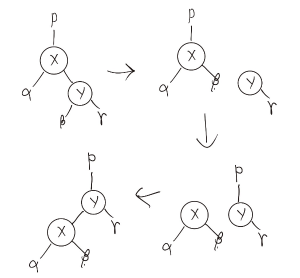
1. LR 회전 (좌우 회전)
   • 왼쪽 자식의 오른쪽 서브트리에 삽입된 경우
   • 먼저 좌회전, 그다음 우회전

왼쪽 회전

오른쪽 회전

1. RL 회전 (우좌 회전)
   • 오른쪽 자식의 왼쪽 서브트리에 삽입된 경우
   • 먼저 우회전, 그다음 좌회전
   • 위의 회전을 반대로 실시

이 회전이라는 것은 우리가 이전에 살펴봤던 RB-Tree의 회전과 같으며 대신 AVL 트리에서는 색깔을 관리할 필요가 없다. 대신 왼쪽, 오른쪽 자식들의 높이차를 이용해 트리의 균형을 유지해야 한다.

요약

• AVL 트리는 "스스로 균형을 잡는" 이진 탐색 트리이다.
• 삽입/삭제 시 트리 높이를 유지하기 위해 회전 연산을 수행한다.
• 덕분에 모든 연산이 O(log n)으로 효율적으로 수행된다.

---

이미지 출처

• https://www.programiz.com/dsa/avl-tree